Rotating, scaling and moving in three dimensions

  • Introduction
  • The Basics: 2D translation, scaling and rotation
  • Isometric, 'true' 3D, and beyond
  • Finished code

    • I've come across some interesting articles on how to do 3D on the net, but in my opinion, none were really explained in the most intuitive way. The purpose of this article is to try and explain exactly what's happening, step by step, so that you can not only create a successful 3D routine, but also understand it - so that you can manipulate and adapt the code into something more.

    Also, you'll discover that the math and logic behind 3D is not as blindingly complex as might first appear. I've done my utmost to keep the code as short and efficient as possible, whilst also making it as easy to follow as possible. As I mentioned earlier, the code I'll use will be closer to something BASIC-ish rather than outright C or machine code. This is so that (hopefully) everyone will be able to understand. Also, you'll need to use floating point arithmetic, because the decimal point is needed.

    What the program will do: In a nutshell, when it's finished, the program will convert a batch of 3D coordinates into '3D-erized' 2D coordinates, so that they can be displayed on the screen.

    What stuff you'll obviously need to start with:
    Numerous object coordinates (X, Y, Z for each object point).

    These coordinates will be manipulated according to the values of the following variables:
    Scroll Offset (X,Y), and Scale (Z), Camera Position (X,Y,Z), Camera Angle (X,Y,Z), Pivot Position (X,Y,Z)
    (The 'Pivot Position' is the point in 3D space at which the camera rotates around when the Camera Angle is adjusted. It's optional and is not required to see 'all possible' views, but is often convenient to more easily set up a specific position or animation).

    The program will use the above inputs (specifically the first 9 variables as the Pivot Position is excluded), and output new 2D coordinates which have been '3D-erized'.

    The only thing you'll need to figure out on your own is how to set up a simple 'screen swapping' routine (double buffer). As it stands, the screen would never clear, so you'd end up with a 'trailing' effect building up on the screen. I assume you're already able to do this in your preferred programming language though :)   [Back to top]


    The Basics: 2D translation, scaling and rotation


    ---TRANSLATION---

    So first things first :) Before we make the leap to 3 dimensions, it's best if I show you how 2D works. The code will be the basic skeleton for the full 3D routine.

    So what shape shall we move and rotate? Well, let's try a simple square. First we define the position coordinates. As we're only in 2 dimensions, we need the x and y location of each point from the square...

    The variables I'll use will be in the form of an ARRAY. Hopefully, you'll know what this is, but suffice to say that they are identical to normal variables with the exception that each variable is 'numbered', so that they can easily be manipulated later on. Observe:

    Sideline: A little note in the syntax I'll use. The "...." symbol effectively means a break in the code to signify a new command or expression. This way, I can squeeze more on a single line, so that you don't have to scroll too far up or down the page. Also, I'll often use 3, 4, 5 or more dots so that the text is nicely aligned. Finally, the number in the middle of the brackets represents the variable array number.

    As you can see, I've given an arbitrary value of -60 or +60 to each of the four points (or corners if you like). This means that each corner will be 120 pixels away from adjacent corners. By the way, the values in these 8 variables are never changed - even when we start moving and rotating. Instead, we store the rotation and movement in separate variables as offsets.

    So then, we want to be able to display this square on the screen, and move it on the X and Y axis (horizontally across the screen and vertically up and down the screen) live while the program runs.
    This is dead easy, and I'm sure you'd work out what to do, but here it is.... Right, hopefully, that should be simple enough. The "X = X(N)+MOVEX" & "Y = Y(N)+MOVEY" lines calculate the final position on the screen that the center of the circle (or whatever) is going to be drawn (n.b. I haven't said "MOVEX = 0 .... MOVEY = 0" , but by default, they are zero at the beginning of the program). For future reference, I'm going to refer to these two very important lines as *SPLAT*. Sounds silly, I know, but it needs to so that you'll remember this reference :P

    Anyway, where were we. The KEY= lines refer to when you press the cursor keys on your PC's keyboard. This should move all four coordinates of the square in the appropriate direction.

    SIZE is an arbitrary number to denote the size of the circle - nothing more. For now, I've given it an arbitrary value of 20 at the very beginning of the program.

    Also, as you can see, the "For" & "End_For" commands make sure all 4 variables of the square in the array are affected together. Finally, the "400" and "300" numbers are arbitrary values to (hopefully) centralize the square on your 800*600 pixel screen. They can be other numbers if you like. Now run the program to see if it works how it should.

    With me so far? Good.

    ---SCALE---

    So we can move the square in all four directions. What else do we need to do? Well, for one thing, we need to scale it - to make it bigger or smaller. This is really easy to do :) Remember those two lines of SPLAT? Just replace the old two lines with these extended versions: The divide symbol ("/") basically closes all numbers in on zero or makes them grow 'away' from zero. This will make the square grow larger or smaller on the screen! When the SCALE variable is very large, all numbers home in on zero, and could be said to approach a 'vanishing point'.

    Also change the circle line from: ...to... With the addition of "/SCALE", the size of the circles will be appropriate - respective to the SCALE zoom level.

    Now, give an arbitrary value of 1 to the SCALE variable, and put this at the very beginning of the program next to the SIZE=30 line (we don't want any divide by zero errors!). Finally, add a couple more key commands with the rest of the key commands, so that you can alter the scale live while the program is running. Something like: That's it! Run the program and experiment with the different keys to see if it works.

    ---ROTATION---

    So now we can move and scale the cube, what else do we need to do? This is the crunch - we need to rotate it about an arbitrary point or pivot. The code for this a bit more complex now, but the good news is that the 2D rotation code for doing this is effectively the same code we need for 3D rotation. In fact, one could say we're already in 3D territory, as we're going to be rotating this 2D square on the Z axis. As you might be able to guess, once we make the full move to 3D, we'll be using practically the same rotating routine for the X and Y axis, as we do here. OK, so this is what we use (deep breath): This code is inserted just before SPLAT (and just after: "For N=1 to 4").

    Yes, I know; it's those evil SINE and COSINE commands ('Cos' and 'Sin'). What? You thought you'd able to escape those? ;)

    Before you faint in terror though, let me give you a description of what this code actually /does/.

    Imagine you have a point at coordinates X(N),Y(N). Picture a circular path coming from this point (yellow point in diagram), and circling around a separate pivot (blue point), eventually reaching back to the point (yellow point). Depending on the angle, what this code calculates is the X and Y offset required for this 'jump' to another position on this 'circle'. So, you input five variables (x+y original point, x+y pivot location, and angle.........., and the math outputs the desired two variables: the new x and y position (or rather, offsets) of the object point). Except you will not have to imagine any longer. A picture is worth a thousand words, so for a clear example of this, look at the diagram. You can skip trying to figure it out, but it's always nice to know what's going on.


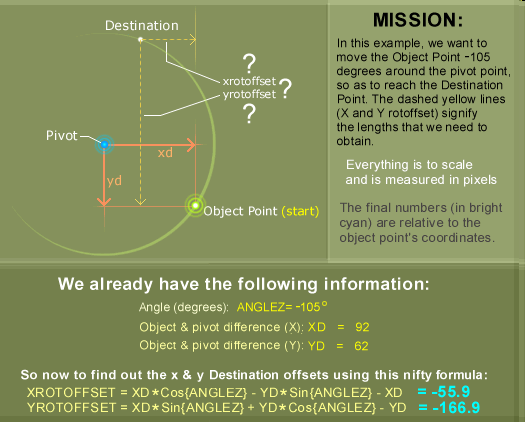
    The code works globally for any point (good news for our square), and all it needs is for us to define the position of the pivot (If you leave out the pivot variables altogether, or define PIVX & PIVY as zero, then the square would rotate around the origin (x=0, y=0), or 'on the spot' in our square's case as it's centered on the origin), and for the angle of rotation (ANGLEZ - default again is zero), and then the code calculates the X & Y offset (XROTOFFSET & YROTOFFSET) automatically. By the way, XD and YD are just temporary variables - used mainly to simplify the look of the code.

    I hope that makes some kind of sense. Don't worry if you don't know how Cosine and Sine combine to magically arrive at the appropriate X and Y offset. The main thing to know is that the code produces two offset numbers which just so happen to be needed in our ever-growing SPLAT routine (I told you SPLAT would come in handy). If you can remember it went from: ....then we added SCALE and we got: Now we've added those awesome rotational offsets, so now it grows to..... By the way, the square brackets I've used represent standard mathematical brackets to separate the math properly.

    Simply replace old SPLAT with this newest SPLAT.

    Just before we move on, we need to add those all-important key command lines, so you can alter the angle and pivot location live while the program is running. The following two lines changes the angle:

    And the next ones changes the location of the pivot. It looks cool when you see the square rotating around a pivot that's somewhere else. As you might guess, by default, the pivot is situated at 0,0 - i.e. in the middle of the square, so normally, the square rotates 'on the spot'. These PIV variables refer to the location of the pivot. This is optional, but we might as well plot a single pixel on the screen so we can see the pivot - and therefore see what we're rotating around. Simply insert the following line after the Draw_Circle line. The math is identical to what we've been through, so I won't bother explaining it:
    Right, we've come this far. I'm going to list the program in full so far:
    Well, Congrats! You've successfully moved, scaled and rotated a square in two dimensions! The fun's just beginning though. We now adapt it slightly to fit into something very closely related to pure 3D - or "Isometric". This is the next step just before we reach true 3D. The difference between isometric and 'true' 3D, is that stuff doesn't get smaller when it goes into the distance. Perspective has no meaning in Isometric mode.   [Back to top]

    Isometric, 'true' 3D, and beyond

    Right, we're into the third dimension now. No more squares - we want cubes! Well, then we'll need to feed the program more coordinates. We'll need more than just 4 points now. 8 points is required to represent each corner of the cube. Replace the old coordinates with this little lot: As you can see, we're just stating the x, y & z position of each cube corner.

    The next thing to do is change the line: to... If you like, you could use a variable to replace "8", and define this variable at the beginning of the program according to how many points you have, but leave it as it is for now.

    ---ISOMETRIC---

    About the only difference between 2D and Isometric is the addition of more rotation code. In other words, we'll need to rotate on the X and Y axis, as well as the old Z axis. Thankfully, the new code is very similar to the code we've already got! Remember that previous Sine/Cosine nightmare? Yes, we return to that :) Previously, it was: From these 4 lines, look at the 3 & 4th long ones. To refresh you memory, this rotates on the Z axis. Now we're in 3D though, can you guess what we add? Yep, two more 'pairs', so that we can rotate on the other 2 axis (X & Y).

    Replace the above 4 lines of old code (shown above) with this new code below. Look to see what's different. Note: XD, YD, ZD, and ZX, ZY, YX, YZ, XY, XZ are simply temporary variables. It's possible to use none of these variables, but it would've been at the expense of clarity (which is paramount at the moment - especially considering the apparent complexity of the routine). What's important to know is this whole routine will output just 3 important variables at the end (the X, Y & Z 'ROTOFFSETs'). Right, initially, it looks ten times worse than before doesn't it? But really, it isn't all that bad. As you can see, there are 3 'pairs' now (look at the ZX= & ZY=, YX= & YZ=, XY= & XZ= to represent the 3 axis). But why does the code for the YX= & YZ= pair of lines seem to be longer than the old ZX= & ZY= pair? And why are the XY= & XZ= pair of lines longer still? It's a good question, because one would expect each pair to be the same length. In fact, it's got nothing to do with the fact that the X axis (XY & XZ - third pair) is more 'special' than the Y or Z axis. The real reason is because each pair has to take a variable from the calculation of the pair that preceded it.

    In fact, the above code is just one of six possible configurations. I could have chosen five others, and the code would effectively execute the same thing.

    Let's take another look at the second pair (YX= and YZ= lines): After closer examination, you'll see what's been 'added'. In the first part "[XD+ZX]", the "ZX" has been added to the sum. It's also been tagged on to the end of the first line too. It turns out that ZX is one of the variables from the /first pair/. It is added to the amount in this second pair because the math has to take into account the previous calculation. It can't just work out the sines and cosines of certain angles - it also needs them to work on the sines and cosines of calculations that have already been made, so that a 'master' offset rotation can be figured out. The same reasoning applies to the third pair too - in this instance, variables taken from the preceding first /and/ second pairs are used in the math.

    Other changes from the old rotation code include the line: ZD = Z(N)-PIVZ ...and also the three lines:
    XROTOFFSET = YX+ZX
    YROTOFFSET = ZY+XY
    ZROTOFFSET = XZ+YZ

    These 3 statements simply add up all the 'rotational offsets', so that they can be used in the final SPLAT conversion routine.

    Now just to add the usual keys, so that we can change the angles live while the program is running. We already have this:
    ..Now add these new ones:
    The above should hopefully be self-explanatory. But just quickly, keys 3 and 4 alter the Y angle, and keys 5 an 6 alter the X angle.

    That's it for isom! A second congratulations is in order. You should now be able to 'rotate' the cube in all 3 dimensions!

    There's something not quite right though - something 'fake' about the way it's rotating, which moves us on to:

    ---'True' 3D---

    This is the real thing. No more boring squares, no more fake cubes. Now we have Horizon and Parallax! Perspective! Camera location and angle! New variables! More opportunity for dividing by zero! (ummm... skip that last one ;)

    The rest of this tutorial will not add or change anything significantly to the existing code. Instead, we'll be adding little bits here and there, so that everything conforms to real 3D. I still like the isometric routine though, so there will be occasions where I won't replace code, but use an 'If' routine so that we can toggle between Isometric and Real 3D at will. In fact, we can do something about this now. Add this line at the start of the program: When MODE is equal to 0, we'll still be in Isometric, and when it's changed to 1, we'll be in proper 3D. Add this following piece of code along with the other key commands, so that we'll be able to change to 3D while the program is running: The code 'Wait 2' means that the program won't switch between Isometric and 3D a million times a second. You might want to use something more efficient (such as the program knowing when the key has been let go). "Else" means to execute the code below it, if MODE wasn't equal to zero.

    The rest should be self explanatory. But hold your horses though - we haven't even defined what the CAMZ variable is yet, let alone why we need those SCALE=SCALE*/CAMZ lines. Suffice to say that the program will work without them, but unless we have them, the scale will go awry (massively too big or small) when we swap between the Isometric/true 3D modes while the program is running.

    As for the CAMZ variable, well, this leads us nicely onto the Camera location...

    ---CAMERA---

    We need a position for the 'Camera'. In other words, we need to define how far everything away is. For now, insert this code at the beginning of the program: Because we're in true 3D, if CAMZ equalled 0, we'd be /INSIDE/ of the cube, and barely be able to see a thing - if at all. At 300 though, we can see the action at a distance. CAMX and CAMY can remain at zero of course.

    Now we pay a final visit to SPLAT (you knew that would come again sooner or later, didn't you).

    Currently, SPLAT looks like this: ...But now we now change it to incorporate the camera position and Z dimension stuff. Remember how I said I wanted to keep the old Isometric code as well as incorporating the new true 3D code? Well, we'll need to add an "If" statement because of this. Observe: Aha! Take a look a the last 3 lines (Z, X & Y). Now we've just had a glimpse of the new /Z/ variable. It's needed to take into account the 3rd dimension, and also effectively provides us with a 3D vanishing point (more on that in a bit).

    Also, notice how the CAMera X and Y variables are /inside/ the brackets, while the normal movement variables (MOVEX and MOVEY) are /outside/ as usual. This is done because we're not just 'scrolling' a flat 'piece of paper', but instead moving the camera 'properly'. This way, we'll notice that the cube moves in /parallax/ (where the front of the cube seems to be moving more quickly horizontally/vertically across the screen, than the back). Naturally, we'll still be able to 'scroll' the scene in the old 'flat piece of paper' way (MOVEX & MOVEY) via the cursor keys, so we'll add different keys to move the camera around in a moment.

    So let's take another look at this Z variable. Here again, are the three crucial lines of code: Another thing that was added to the old SPLAT that's clear to see. As well as dividing by SCALE, we're now also dividing by the Z variable. This is because we're now taking into account another factor which determines how close an object point is to the 'vanishing point'. Before, only the SCALE had to be enlarged for all object points to move towards one tiny area of the screen (i.e. towards the vanishing point). But now there's another way. Now, an object point can be further back in the Z direction, and therefore, it will /also/ be closer to the vanishing point. This is more commonly known as 'perspective'. Because of this, we use the first Z line to determine exactly how far into the distance that an object point is, and then divide by Z in the last two lines. Clever huh? If you're still confused, see the following diagram for a clearer explanation on how the new Z perspective works.


    Right, that's just about it for SPLAT you'll be glad to hear. It's been through 4 different stages - each with increasing complexity, but it'll go through no more. *SPLAT is complete*

    So what next? To account for this new way of Camera 'moving', we'll need four more keys. I know - instead of using the cursor keys, we'll use the arrow keys of the keypad (which are 2, 4, 6, 8 ).
    Add to the key press lines the following: Almost there now!

    The last thing we need to change is the circle line of code. Before, it looked like this: ...But now change it to the following: You'll be familiar with how Z determines how far into the background an object point is, because it's the same line of code that we just used for the SPLAT routine.

    Do you remember that line of code which displayed a pixel on the screen to represent the pivot? Well, here it is anyway: Now we change it slightly to take into account the Z dimension. Once again, it displays the true pivot, so that you can see exactly what you'll be rotating around. Replace that single line with the following 3 lines: You're never going to believe this. We're all done!!! Now, before you excitedly try it out, let's take a final look at the whole program. Lines that use ">>>" at the beginning are quote lines so that I can mention what part of the code it is. I'll 'close' with arrows going left (i.e. "<<<") to signify the end of that code part. Congrats - you now have permission to run your program to experiment! Once you're done, you might want to add a magic piece of code just after the "START_LOOP" line: This should make the cube rotate automatically! Now we have an all singing, all dancing cube. Is there anything left to do?
    Well, it goes without saying that you can feed just about any shape into the program. There's nothing to stop you from rotating and moving dodecahedrons or entire game-scapes if you so desire (and if your pc is fast enough ;)
    As an exercise for the reader, try to build up a 1,000 point 'cube' (10*10*10) points by adding a relatively small amount of code to the beginning. The effects of 3D look spectacular when there are so many points to rotate and move through! /Especially/ if your PC is fast enough to display everything in 50 FPS (frames per second) realtime.

    At the moment, the program uses simple circles, but it shouldn't take too much effort to replace these circles, and have lines joining up to make a wireframe cube. Apart from that, we could explore using matrices, solid shading, texture mapping, even gouraud shading, light sources and 4D+. We'll leave all that for another time though...

    Well, I hope I've made it an interesting and informative article! Please let me know if this article has helped you understand 3D a bit better. Also, if there's something I should edit to make clearer, then I'd be interested to know how.   [Back to top]

    And now for something completely different...
    You've learnt how to program a cube, now learn how to draw one with this excellent tutorial at Castlezzt.net (original link was down from here, so this is a mirrored version, but the original creation was castlezzt.com).



    If the info on this site has been of sufficient interest, a small donation would be appreciated:
    Amount you wish to contribute:



    Message your comments to the Skytopia Forum
    or email here